[信号与系统] 第二章 线性时不变系统的时域分析
第二章 线性时不变系统的时域分析
0、LTI系统的定义
Linear Time-Invariant (LTI)
如果一个系统既线性,又时不变,我们就叫它线性时不变系统。

线性时不变系统的性质
为什么研究线性时不变系统?
为什么研究线性系统
首先思考一个问题:这个世界上有绝对意义上的线性系统吗?(满足齐次性和叠加性)
满足齐次性就意味着如果一个系统是2x,那么假设通入1A的电流,输出就是2A。但是所有物理组成的系统,都有它的上限。(你通入10000A的电流,输出还会是20000A吗?)它由于物理的限制,必定有其上线。
比如喇叭和麦克风,A说一句话,喇叭就原封不动的重复这句话。但是实际上声音肯定会有失真。
所以说没有绝对意义上的线性系统。
那么为什么要研究线性系统呢?
因为现实过于复杂,线性是对现实合理化的近似。
例如上面电流的系统,在一定范围内,可以看成是线性的。
喇叭和麦克风在一定程度上,也可以看成是线性的。
从这个角度看,大部分现实中的系统,在一定程度上,都可以把它看做线性系统。
(与其说世界上的模型大部分是线性,不如认为我们没办法处理过于复杂的模型,只能把世界上的事物近似成线性模型来分析)
为什么研究时不变系统
继续思考一个同样的问题,这个世界上有完全的时不变系统吗?
(时不变系统,意味着无论什么时候给出同样的输入,它都会给出同样的输出)
当然在物理世界内这个也是不可能的,电机会老化!设备会老化!没有什么东西是永远的。
所以说没有绝对意义上的时不变系统
但是,时不变系统是对真实世界的合理假设。
如果你要把系统看成时变的,那么物理将不存在,今天给出一个结果,明天给出另外一个结果。我们无法做研究了。
就像一块肉,放在室温下会腐烂,但是在某段时间内,我们研究它,肯定要把它当成时不变的系统来才行。
LTI系统很简单
因为这个系统很简单,所以我们研究它。
它简单到如果我们知道LTI系统的一个x(t)对应的输出y(t),那么我们就知道了所有的x(t)对应的y(t)。
第二章讲的所有内容,就是为了表明这句话!
1、线性时不变系统的性质(复习)
Note
我们先来复习一下线性系统和时不变系统的定义
线性系统:
1.齐次性:任意的x(t)经过系统变为y(t),则ax(t)经过系统变为ay(t)。
2.叠加性:任意的x1(t)经过系统变为y1(t),x2(t)经过系统变为y2(t)。则ax1(t)+bx2(t)经过系统变为ay1(t)+by2(t)。
时不变系统:
- 经过系统变为$y\left( t \right) x\left( t+t0 \right) y\left( t+t0 \right) $
根据这两个性质我们来做一到题目:
假设有一个离散的$x\left( n \right) y\left( n \right) x\left( n \right) \tau \left( n \right) y\left( n \right) $是一个分段函数,
那么如果输入是$2\tau \left( n \right) $输出会是什么呢?

图1
那么这个问题结果就是原来的$y\left( n \right) $ 上面的每个点乘以2。(因为线性系统的齐次性,输入扩大两倍,输出也扩大两倍)
那么如果输入是$\tau \left( n-1 \right) $输出会是什么呢?
这个问题的结果就是输出右移1个单位(因为时不变系统的性质)
那么如果最后根据叠加性出一道题目的话
输入如果是$2\tau \left( n \right)+\tau \left( n-1 \right)$的话,它的 输出就是第一道题目和第二道题目加起来!
再来看一道稍微复杂的题目:
输入如果是下图这样,输出会是怎么样的?

图2
2、卷积
我们定义这个特殊的序列$x\left( n \right) =\delta \left( n \right) $称其为单位脉冲序列。

图3
单位脉冲序列经过系统,得到的输出,我们有个专门的名字,叫做$h\left( n \right) $,称作"单位脉冲响应"。
对于LTI系统,单位脉冲响应$h\left( n \right) h\left( n \right) $,我们可以计算出任意一个输入的输出响应。就如果我们之前那道题目里做的一样。
假设这个输入为$x\left( n \right) y\left[ n \right] =x\left[ n \right] *h\left[ n \right] $。
这个就是卷积(convolution)。
来几个判断:
如果两个LTI系统的$h\left( n \right) $一样,那么这两个系统就是一样的。
(换句话来说,因为$h\left( n \right) $一样,所以这两个系统对于同样的输入,就有同样的输出!同样的输入有同样的输出,这两个系统就一样吗?这个是个哲学问题。我们一般认为,如果看上去像鸭子,吃起来像鸭子,叫声像鸭子,它就是鸭子。)
换句话说,$h\left( n \right) h\left( n \right) $里面。
3、卷积的计算(离散)
那么如何计算$x\left[ n \right] *h\left[ n \right] $呢?
3.1列表法(略)
首先,确定$y\left[ n \right] =x\left[ n \right] *h\left[ n \right] $取值范围。
的最左边等于$x\left[ n \right]$的最左边加上$h\left[ n \right]$的最左边。
的最右边等于$x\left[ n \right]$的最右边加上$h\left[ n \right]$的最右边。
这部分内容我能够理解,但是用文字讲不太清楚,反正最后卷积公式是:
实际上这个就是列表法定义,只是把定义用数学语言描述出来而已。
4、连续LTI系统卷积公式
用卷积的性质做几道题目(LTI性质不保证放缩哦):

题目
这里就是需要问一个问题?如果最后的输入信号是一个任意的,那么经过同一个LTI输出是什么?
我们无法回答这个问题:
但是如果用一个阶梯函数近似:
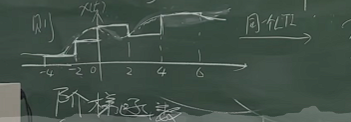
阶梯函数
我们可以知道这个阶梯函数的输出。也就是近似的输出。
这个近似太不精确了吧,每隔2个单位,才有一个阶梯。
为了让近似更加精确,假设我们不是0~2的输出,而是0~1的输出的响应,可以得到更加近似的阶梯函数:
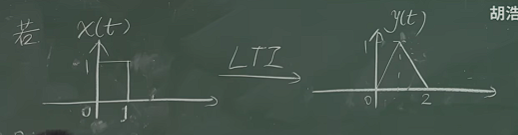
1个单位的近似
所以我们想探寻一个无线窄的方波,对应的响应是什么。
当δ无线接近0的时候,高度为1/δ,就是一个冲击。
我们如果用冲击去构建前面的阶梯函数,就可以把前文提到的离散的卷积变成连续的了。
区别就是从级数和变成了积分。
这里文字描述起来,我不知道怎么讲,看视频的话,应该是比较明白的。
(里面没有数学推导,你到后面发现这个就是黎曼积分的定义)
4.1冲击响应的性质
这部分比较困难,1833年有了极限的概念为了证明这部分性质,但是极限真正完善是到1907年左右。中间有大概70年左右的时间。
也就是说世界上最聪明的大脑都花了70年才想明白这些问题,作为一个普通的学生,想不明白这些问题是很正常的。
根据胡浩基老师的课程所述,需要学实变函数和泛函分析,所以详细的证明略过。(老师大概花了1个小时在介绍勒贝格)
我们需要首先介绍一名数学家,他叫做勒贝格(开创实变函数和泛函分析)。
他是一名中学老师的,当他开创实变函数的时候,也是从中学的问题开始想起(用的都是中学的知识)。
“两个函数$f1(t)$和$f2(t)$什么时候相等?”
中学的时候,定义这个问题:若任意的T0属于实数域,$f1(t0)=f2(t0)$则两个函数相等。
但是勒贝格觉得这个定义太过于严格了。他重新定义了相等
....
PS:总之很复杂,我也不会证明,下面的性质直接用即可。
4式是5式的特例。我们根据这个性质来算几道例题。
例题1:$\delta \left( t^2-3t+2 \right) $
直接把公式代入进去即可:
例题2:$\int_{-2\pi}^{2\pi}{\left( 1+t \right) \delta \left( \cos t \right) dt=?}$
先利用5式算$\delta \left( \cos t \right) t=\frac{\pi}{2}+k\pi \text{时}\delta \left( \cos t \right) =0\text{,}$
然后代入,可以知道$\frac{1}{\left| f\prime \left( t_0 \right) \right|}$这一项恒为1
所以最后结果为: $\sum_{k=\text{整数}}{\delta \left( t-\frac{\pi}{2}-k\pi \right)}$
这个冲激函数的图像为:
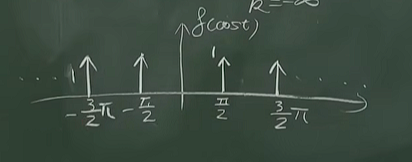
该函数的图像
在-2π到2π之间取值,只有4个值,最后得到下面这个公式。
也就是:
在用2式,可以得到:
原式子就是:
4.2 冲击函数的多样性
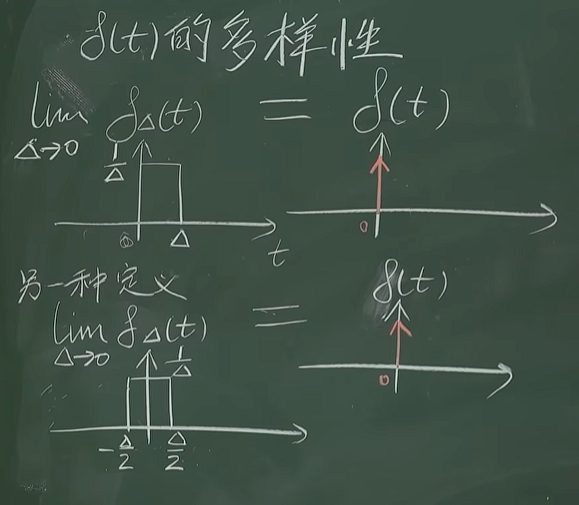
δt的不同定义
冲激函数的定义可以是多种多样的,只要满足对任意的函数y(t)都可以实现
根据公式2就可以知道f(t)是冲激函数了。(用积分中值定理可以证明)
为啥可以把1/δ给提取出来?积分中值定理又是什么?已经忘记了
另外还有一道思考题:
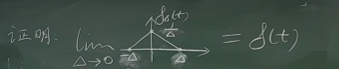
思考题
4.3 冲激函数的重要结论
可以记不住证明,但是请记住下面的重要结论:
下面这个函数也是冲击函数:
它的图像如下所示:
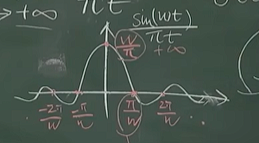
冲激函数
这个是一个往里面无线压缩的Sa函数。
它的积分是1
第三章讲到傅里叶变换的时候会用到它。
这个函数的证明有历史渊源,傅里叶发明傅里叶级数之后,一直没办法证明它的收敛性,直到后来有一个叫狄利赫里(Dirichlet)的数学家才证明了满足一定条件收敛。
在他证明的时候,第一个就是证明了这个公式。
中间过了30年才有人想出来,我们想不出来也很正常。
以下证明为不严格的数学(严格和麻烦)
引理:若$x\left( t \right) \underset{\omega \rightarrow \infty}{\lim}x\left( t \right) \cos \left( \omega t \right) dt=0$并且$\underset{\omega \rightarrow \infty}{\lim}x\left( t \right) \sin \left( \omega t \right) dt=0$
这句话是什么意思呢?我们看$x\left( t \right) \cos \left( \omega t \right) $的图像
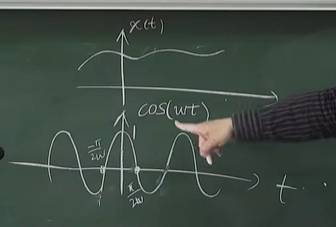
xt的图像
意思到ω取到无穷大的时候(意味着这个震荡会十分的快速), 他们两个乘起来就相当于$x\left( t \right) $变成了包络线。由于这个ω是无穷大,在很小的一个区间内,正的会和负的抵消掉。
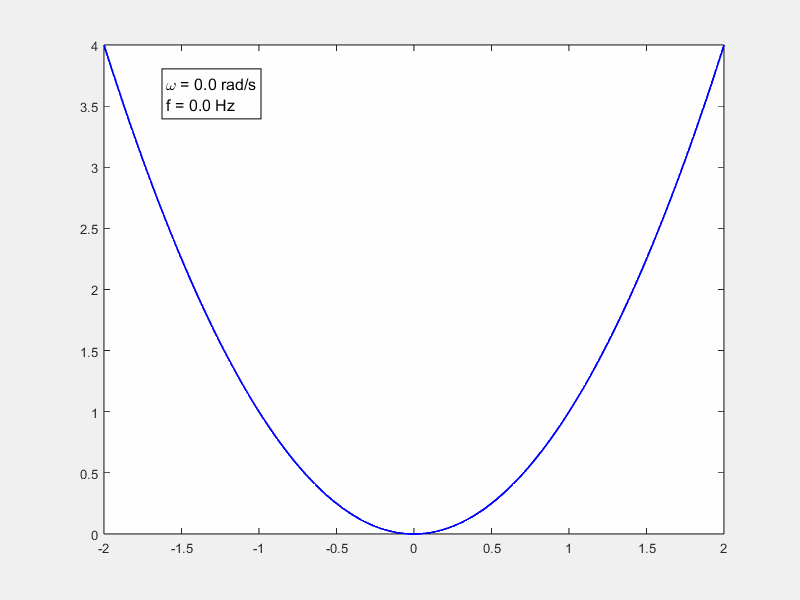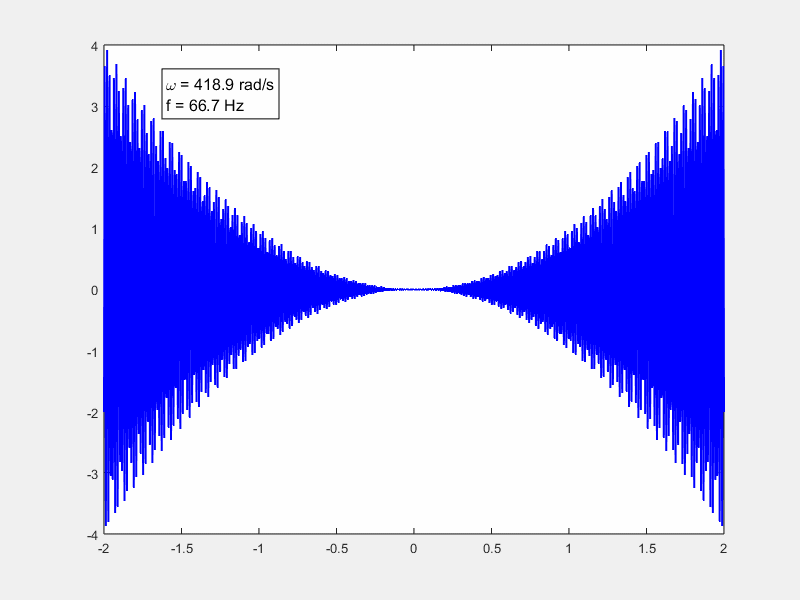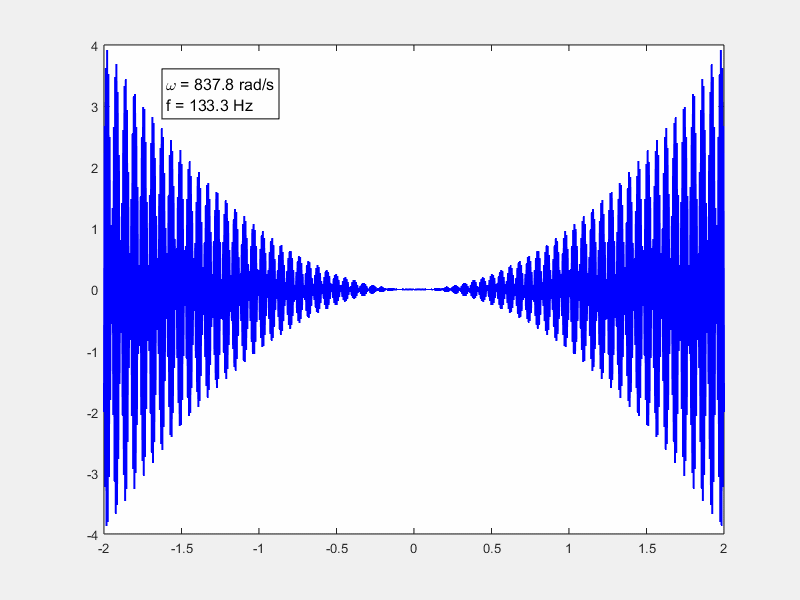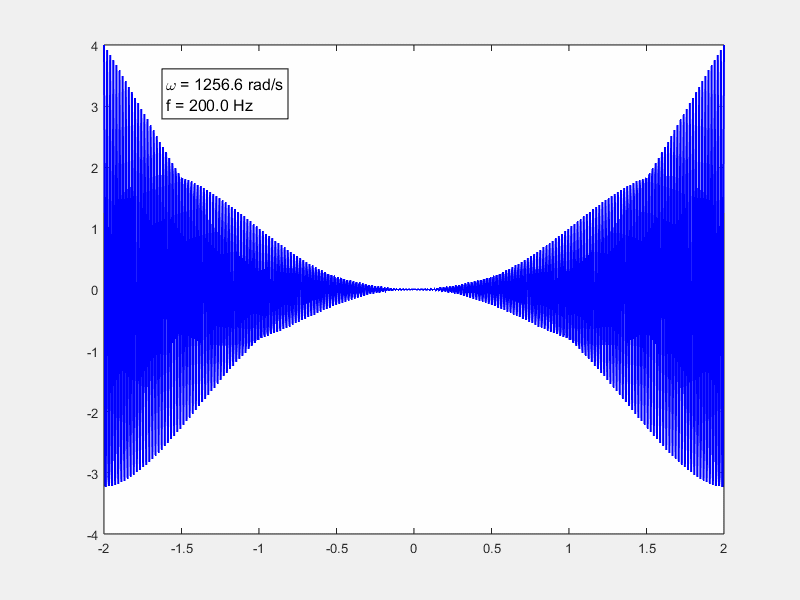
做了一个动图xt是一个二次函数
我们用matlab把积分算一下,可以看到随着ω的增加积分越来越趋于0。这个动画演示的就是由于高频的震荡,导致的积分正负抵消。
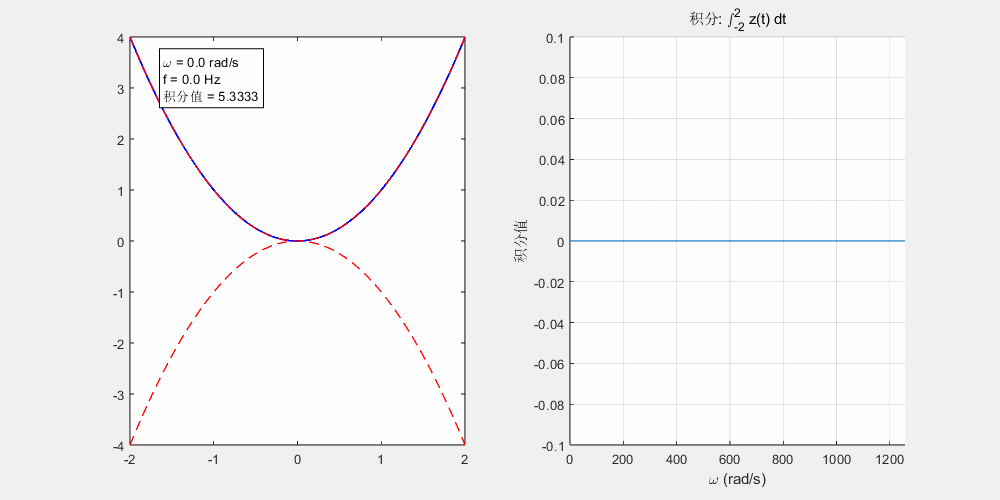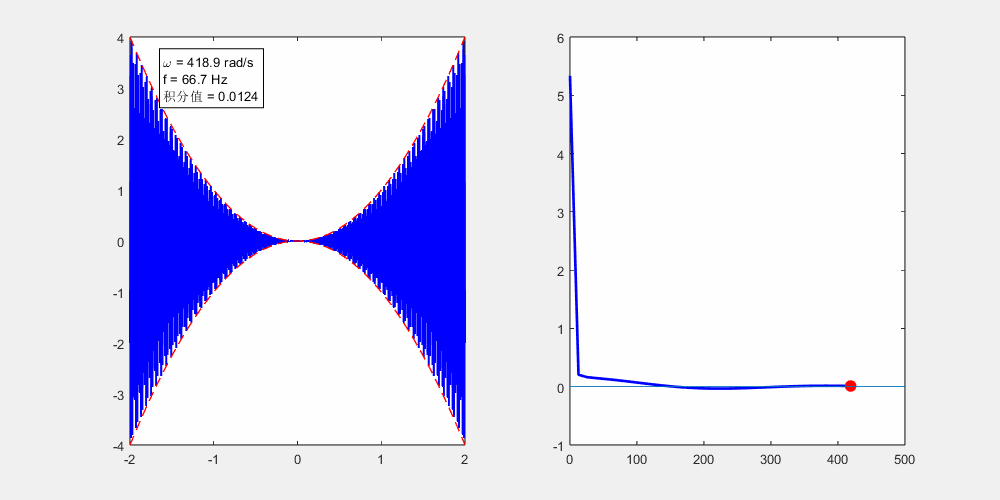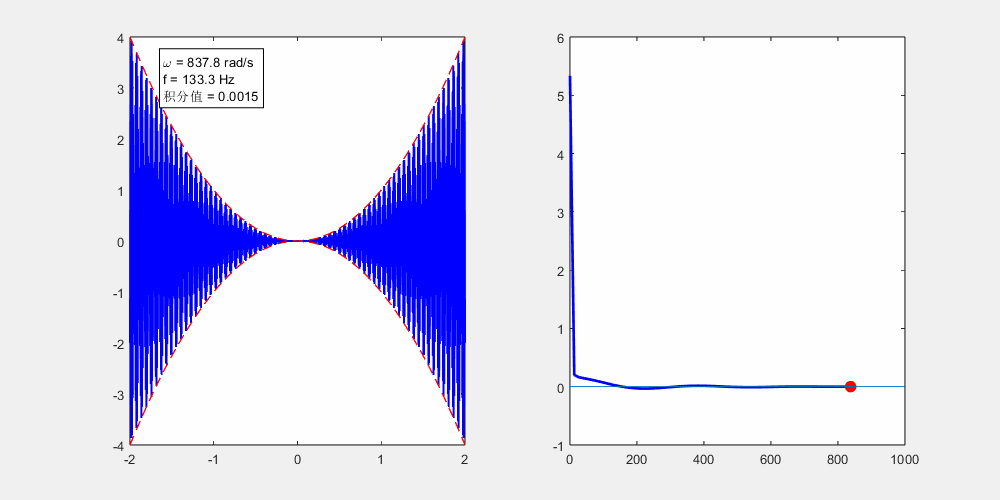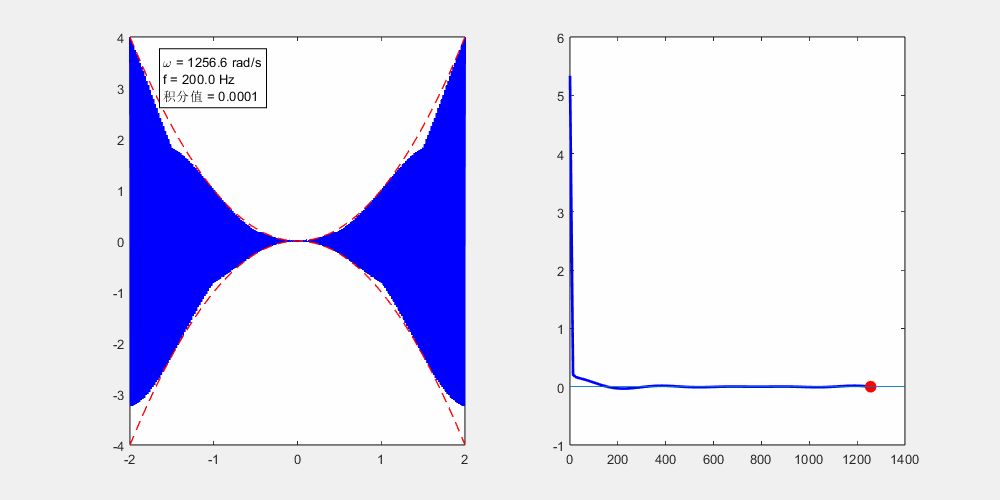
frequency_integral