[信号与系统]第一章
第一章
信号与系统是“数字信号处理”和“自动控制原理”,“现代控制理论”的前导课程。
教材:奥本海默的信号与系统第二版。
学习目的:为了衔接控制领域的课程。
参考的教学视频链接here
我看下来,本章的重点内容就是讲述了正弦信号和一般复指数信号在连续时间和离散时间下的异同。
了解一些一般的信号,在未来的章节中我们会利用这些一般信号,根据线性时不变系统的性质去组成别的信号。
一、正弦信号周期性差异
离散和连续的正弦信号以及一般复指数信号在信号与系统中的差异主要体现在以下几个方面:
1.连续信号的$\omega$越大,则信号震荡速度越快。但是离散信号不是的,它呈周期性变化。
2.连续周期信号,离散后可能不是周期的。
1.连续正弦信号:
连续正弦信号 一定是周期信号,其周期 T0 = $\frac{2\pi}{\omega0}$ 仅需满足频率 。例如, 的周期为1秒。
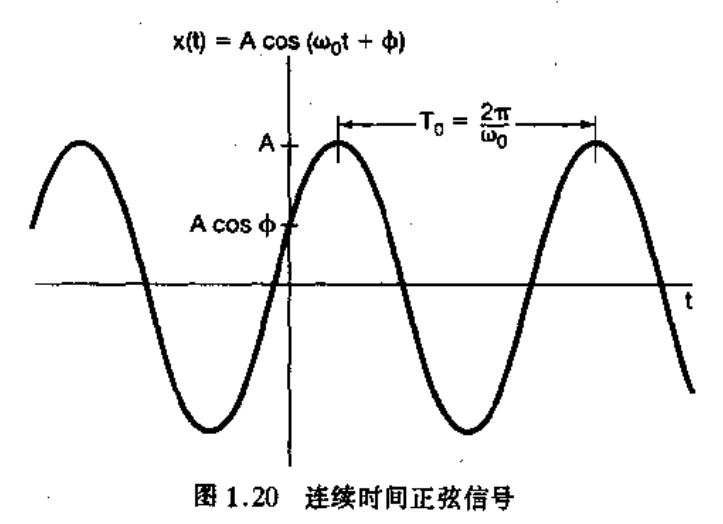
连续时间正弦信号
Important
这里有一个"时移"和“相移”的概念。例如对于$cos(2t)$来说,时移t0的话就是$cos(2(t-t0)$,但是它的相移是 $2t0$,因为$cos(2(t-t0)=cos(2t-2t0)$
2.离散正弦信号:
离散正弦信号 不一定是周期的。只有当数字频率 的比值为有理数(即 ,其中 , 为互质整数)时,信号才具有周期性,基波周期为 ;否则为非周期信号。例如, 是周期的,而 是非周期的。
为什么会这样?我们知道正弦函数是有周期的,而且周期为$2\mathrm{k\pi}$。也就是说对于连续的时间信号, 。这里的意思就是相移$2\mathrm{k\pi}$,正弦信号保持不变。
那么这个对于离散的正弦信号 还成立吗?
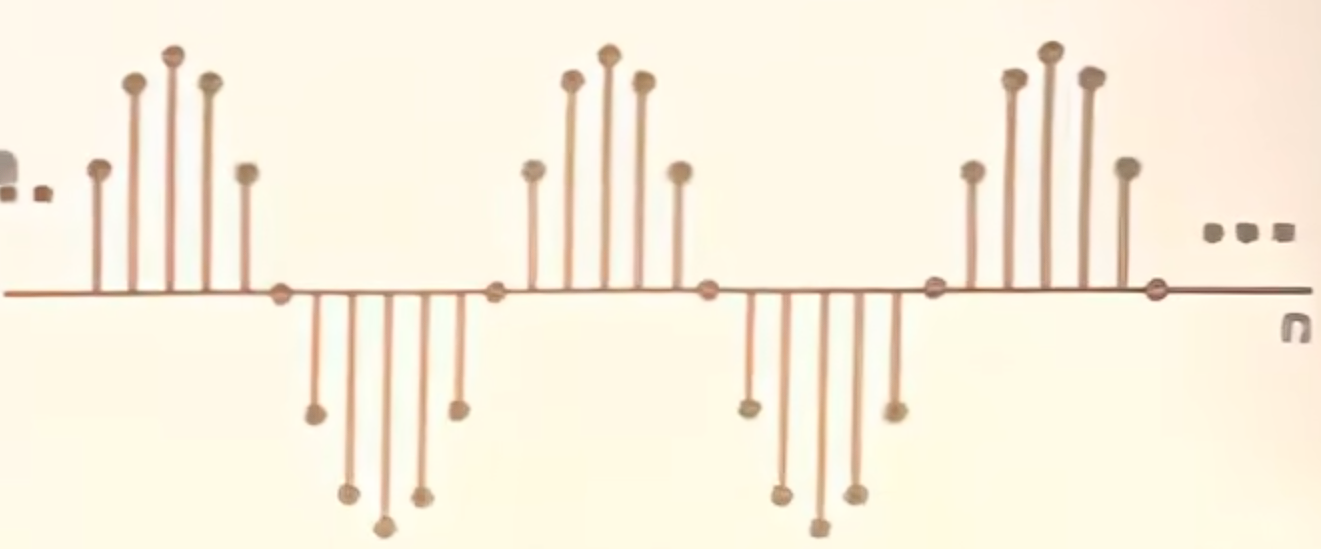
离散下的正弦型号
因为这个序列是离散的,n必须是整数。所以$\omega_0 n$可能不等于$2k\pi$(K也必须是整数)
例如$ \cos(2n)$,它只能取2,4,6,8...这些值,但是这些值永远无法凑出$2k\pi$(k是整数)
所以离散的正弦信号不一定是周期的。
连续周期信号,它的离散不一定是周期的。这个结论有点反直觉。
二、正弦信号ω变化时的差异
连续的周期信号随着$\omega_0$的增加,基波周期会越来越小。
但是离散周期信号不会。如果超过2π就会呈周期性变化,如下图。
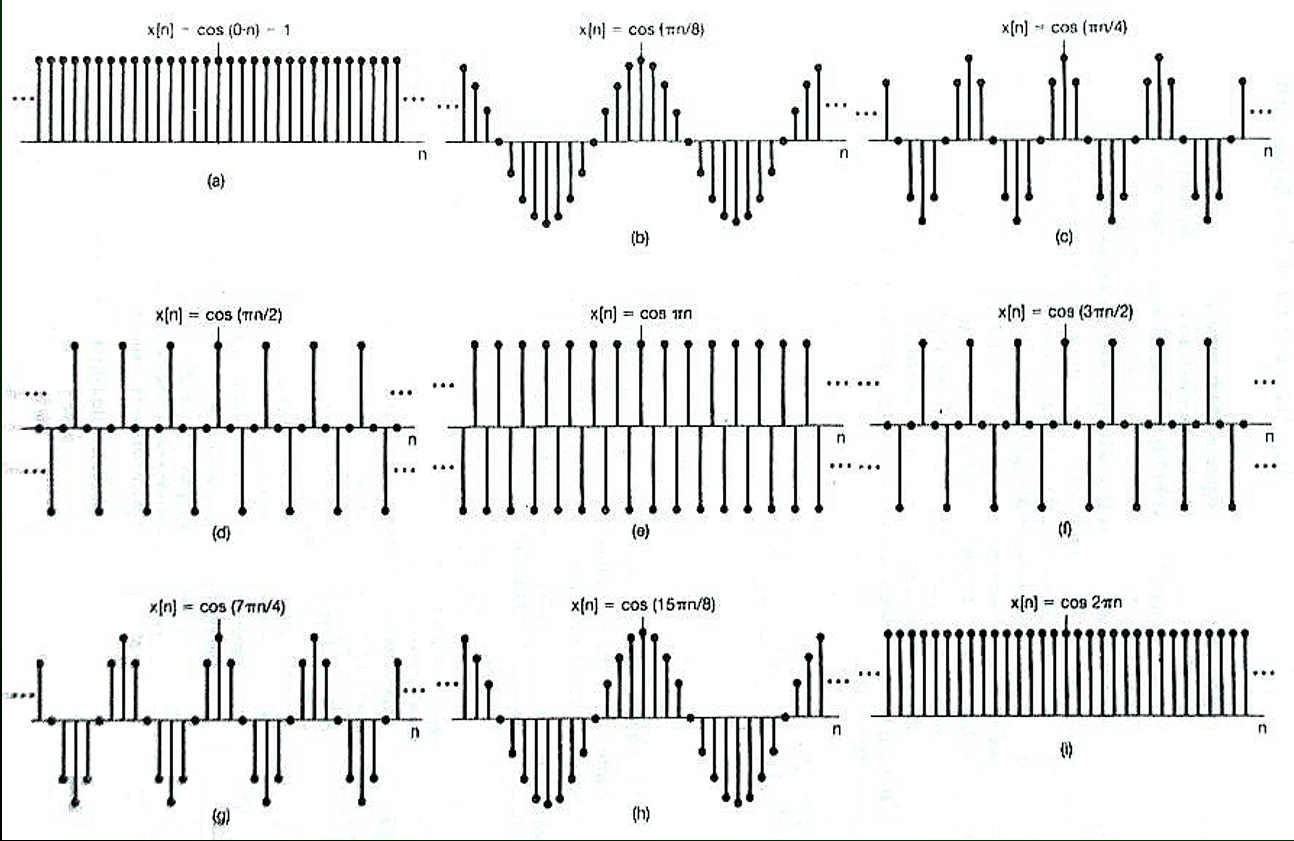
几个不同频率的正弦序列
因为离散周期信号里n为整数,然后它本身又是周期信号,所以最后超出的$2k\pi$部分是可以被$\omega0 n$表示,然后转换的。而连续信号t,它里面除了等于整数的那些点,其他的部分无法满足$2k\pi$=$\omega0 t$,所以自然不会呈周期性变化,而是频率越来越快。
换一个角度,我们可以看上面的这张图片,也可以用图形化的方式解释这个现象。这个现象也是挺反直觉的。
三、复指数信号的形式与参数影响
Important
连续复指数一般用 表示,离散用$x[n] = C \alpha^n$表示
1. 连续复指数信号
- 实指数信号 :当 为实数时, 呈指数增长, 呈指数衰减
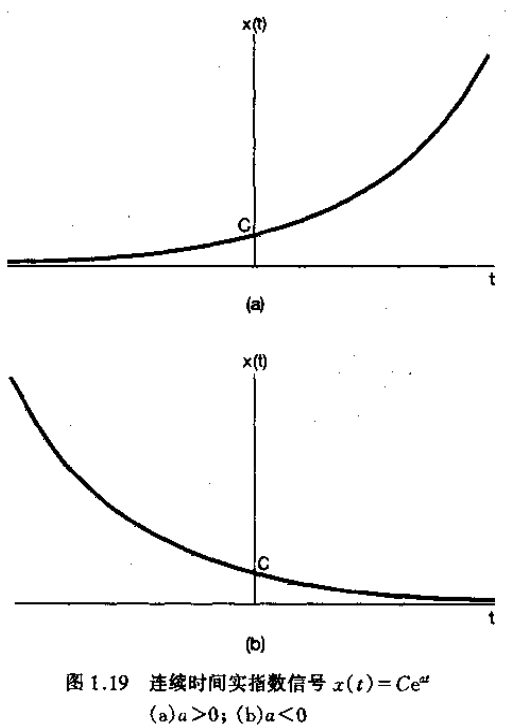
连续时间实指数信号
- 周期复指数信号:当 (纯虚数),信号为 ,对应连续正弦信号的复数形式,具有周期性。
这里引入了虚数的单位。
(我们需要对复数的本质有一定了解,知道为什么有实数,为什么有虚数。例如 。理解这个数字不能朴素按照次方的思路去解释,例如$ e^{n}$就等于e*e这个操作进行了n次。但是 不是这样子理解的,实际上这个是在复平面上按照角速度$\omega0$做旋转。关于这部分的理解可以参考3BlueBrown的视频[here](https://www.bilibili.com/video/BV1G4411D7kZ/?sharesource=copyweb&vdsource=b1475488c94a2443339f39608362cd6b))
- 一般复指数信号:若 ,则信号为 ,表现为振幅按指数增长( )或衰减($ \sigma < 0$ )的正弦振荡。PS:它实部或虚部的图像如下所示:
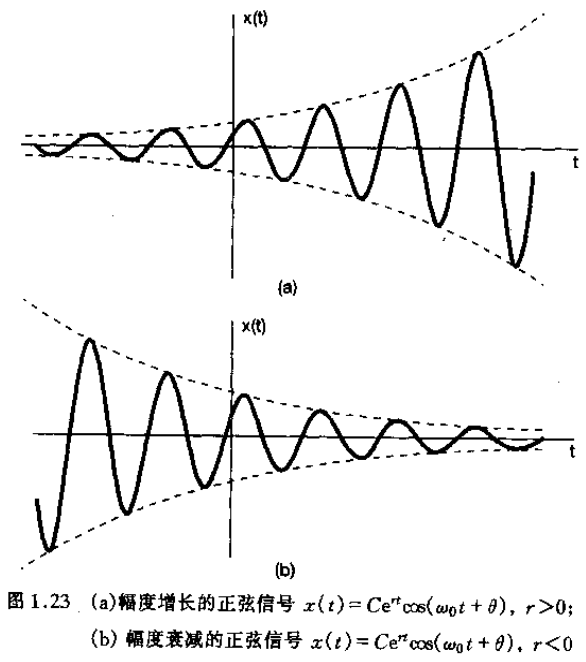
连续时间一般复指数信号Re或Im
1. 离散复指数信号
形式为 (离散这个表达式更加方便),其中 为复数。根据 的模长和相位:
- 实指数序列:若 为实数, 时序列单调增长, 时单调衰减, 时符号交替变化。
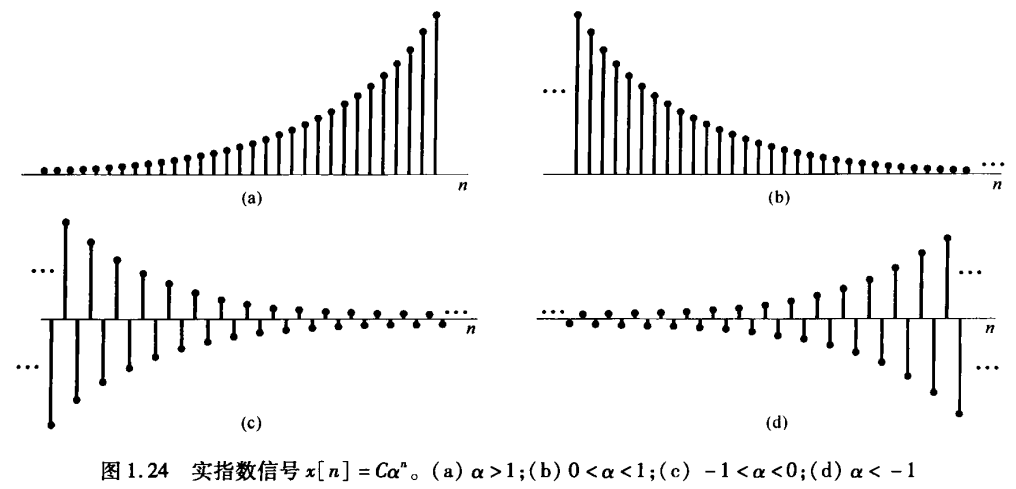
实指数信号
周期复指数序列:若 ,则 ,其周期性与离散正弦信号的条件一致,需满足 为有理数。
一般复指数序列:若 ,则表现为振幅按 增长($ r > 1 r < 1$)的正弦振荡。
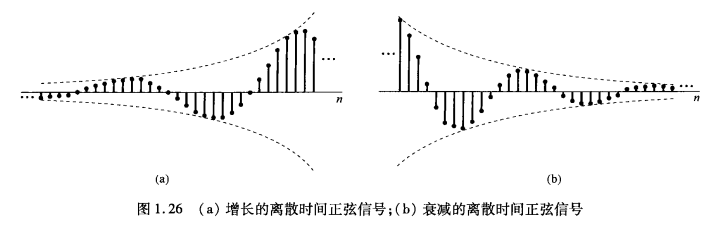
image-20250405171641092
四、单位冲击与单位阶跃函数
冲击和阶跃是另外两组基本的信号。
1.离散情况下
单位脉冲(unit impulse)可以表示为:$$\delta \left[ n \right] =\begin{cases}
0,n\ne 0\
1,n=0\\end{cases}$$
单位阶跃(unit step)可以表示为:$$u\left[ n \right] =\begin{cases}
0,n<0\
1,n\geqslant 0\\end{cases}$$

image-20250407223804152
他们之间的关系为:
这个结论用数形结合可以判得
2.连续情况下
单位阶跃函数:$$u\left( t \right) =\begin{cases}
0,t<0\
1,t>0\\end{cases}$$
单位冲击函数:$$\delta \left( t \right) =\frac{du\left( t \right)}{dt}$$
离散情况下,冲击和阶跃的关系是"求一次差分"与"求和"。
在连续情况下就变成了"求一次微分"和"积分"。
(但是实际上由于阶跃不连续,在t=0出没有值,所以无法求导,我们这里是近似的看待。在数学理论上不严谨,但是我们工程上能够理解这种概念即可)
五、系统基本性质
线性系统、时不变系统,因果系统,稳定系统,无记忆系统,可逆系统。
什么是系统?
给一个输入,经过一个黑盒子,有一个输出。那么这个黑盒子就是系统。
可以说系统无处不在。
有的情况下,我们已知一个系统,希望根据输入去预判输出。
在自动控制这个领域中,我们更加希望的是,能够根据我们对输出的要求(例如超调,响应时间,衰减多少db),然后去设计一个系统,调整一个系统,让输出能够满足我们的设计指标。
那么在信号与系统作为它的前导课程,给出了系统的几种简单的性质。
关键是“线性”和“时不变性”,其他性质简单了解即可。
- 线性系统
齐次性定义:假设任意x(t)经过某个系统得到y(t)。则有:ax(t)经过同样的系统得到ay(t)。
叠加性定义:x1(t)得要y1(t),如果x2(t)得到y2(t)。则有x1(t)+x2(t)得到y1(t)+y2(t)。
如果齐次性和叠加性同时满足,则该系统为线性系统。
例如一个放大器(y(t) = 3x(t))就是一个线性系统。
只需要分别证明它的齐次性和叠加性即可。
而一个 y(t)=x(t)+1这个系统,就不满足齐次性的定义,不是线性系统
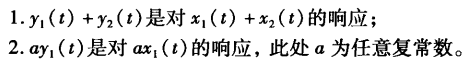
可加性和比例性
两者结合:
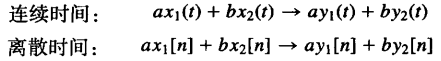
线性
由该性质可得:

叠加性质
- 时不变性

时不变性
- 记忆性
无记忆性是指,对于自变量的每个值,输出仅取决于该时刻的输入。
下面这个例子就是无记忆系统
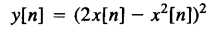
无记忆系统
而下面这个就是有记忆系统
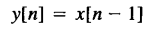
有记忆系统
- 可逆性
如果不同输入,导致不同的输出,则该系统可逆。
下面这个就是一个可逆系统
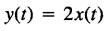
可逆系统
下面这个就是不可逆系统
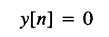
不可逆系统
- 因果性
因果性是指一个系统,任意时刻的输出只取决于现在以及过去的输入(无记忆系统一定是因果的)
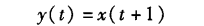
非因果系统
这种系统是非因果的,因为未来是不可预知的。
- 稳定性
这部分可以看参考的教学视频,里面教授用他儿子的玩具给我们展示了什么是稳定性,以及如何通过反馈去让一个不稳定的系统稳定。这个也是我们在控制中希望做到的。
【奥本海姆《信号与系统》 【精准空降到 42:41】 https://www.bilibili.com/video/BV1SB4y1C7yx/?p=3&share_source=copy_web&vd_source=b1475488c94a2443339f39608362cd6b&t=2561
定义:如果x(t)有界,则y(t)也有界
连续微分器:不稳定
离散微分器:稳定
叠加器、积分器:不稳定

image-20250616224730780
疑问
1.为什么离散中$x[n] = C \alpha^n$这种表示方式会比$x(n) = C e^{an}$方便?
如果在连续函数中,用$x[t] = C \alpha^t$,当 的时候,t为分数的时候,图像会在复数域上,要用四维的坐标来表示。而离散情况下,因为n只能是整数,所以没事,可以画出它对应的图像。
同样,要让$e^{an}<0$要有虚数的出现,貌似本书的作者认为有虚数出现会不方便。所以在离散中采用了$x[n] = C \alpha^n$这种表示方法,然后讨论α的值。
2.思考。我们知道,一个线性系统的定义是满足齐次性和叠加性。那么是否能找出一个例子,它满足叠加性,但是不满足齐次性呢?
3.快速判断依据
线性系统快速判断依据:
1.每一项都有x。
2.每一项的x都是1次。
时不变系统快速判断依据:
1.t只在x的括号内。
2.t只能是t,不能是2t,-t等其他函数。
因果系统判断依据:
1.y自变量恒小于x的自变量